静電場の基本法則1
電磁気学の法則であるGaussの法則に対して、Gaussの定理を適用することによって、積分記号が外れ局所的な表現が得られる。
\begin{align}
\nabla\cdot\bm{E}(\bm{x}) =\frac{\rho(\bm{x})}{\varepsilon_0}
\end{align}
これは静電場の基本法則といえる。この方程式に関しては時間変動を考慮してもこのまま成立するため、Maxwell方程式のうちの1つがようやくここで導出できる。
\begin{align}
\nabla\cdot\bm{E}(\bm{x},t) =\frac{\rho(\bm{x},t)}{\varepsilon_0}
\end{align}
Gaussの定理とGaussの法則
Gaussの法則より、任意の閉曲面$S$に囲まれる領域$V$に対して、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n}\, \dd S=\frac{\int_V \rho(\bm{x})\, \dd^3 x}{\varepsilon_0}
\end{align}
が成立する。一方で、Gaussの定理を左辺に利用することで、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n}\, \dd S=\int_V \nabla\cdot\bm{E}(\bm{x})\, \dd^3 x=\frac{\int_V \rho(\bm{x})\, \dd^3 x}{\varepsilon_0}
\end{align}
となる。ここで、領域$V$は任意にとれるため各点$\bm{x}$において、
\begin{align}
\nabla\cdot\bm{E}(\bm{x}) =\frac{\rho(\bm{x})}{\varepsilon_0}
\end{align}
が成立し、表式を得る。
静電場の基本法則1
Gaussの法則に対して、Gaussの定理を適用して得られた微分形のGaussの法則:
\begin{align}
\nabla\cdot\bm{E}(\bm{x}) =\frac{\rho(\bm{x})}{\varepsilon_0} \label{eq: static_E_law1}
\end{align}
は、静電場を決定する基本法則といえる。これは、これまでのCoulombの法則やGaussの法則のような遠隔作用による表現ではなく、近接作用の表現になっている。すなわち、位置$x$方向にだけ電場が変化する場合、
\begin{align}
E_x(x+\Delta x)=E_x(x)+\frac{\rho(x)\Delta x}{\varepsilon_0}
\end{align}
のように$x+\Delta x$と$x$の電場が関係づけられている。そして、その電場を変える要因となるのが電荷の存在であり、位置$x$の電荷密度$\rho(x)$の分だけ変位するようになっている。
この章では静電場のみを扱うため、時間変動については考えていない。ただし、電荷密度が$\rho(\bm{x},t)$と表せる場合、それに従って電場も$\bm{E}(\bm{x},t)$と変化するとして、
\begin{align}
\nabla\cdot\bm{E}(\bm{x},t) =\frac{\rho(\bm{x},t)}{\varepsilon_0} \label{eq: maxwell_gauss}
\end{align}
のようにそのまま拡張できる。これは、電場を決定する基本法則であり、Maxwell方程式の1つ目がここで得られた。
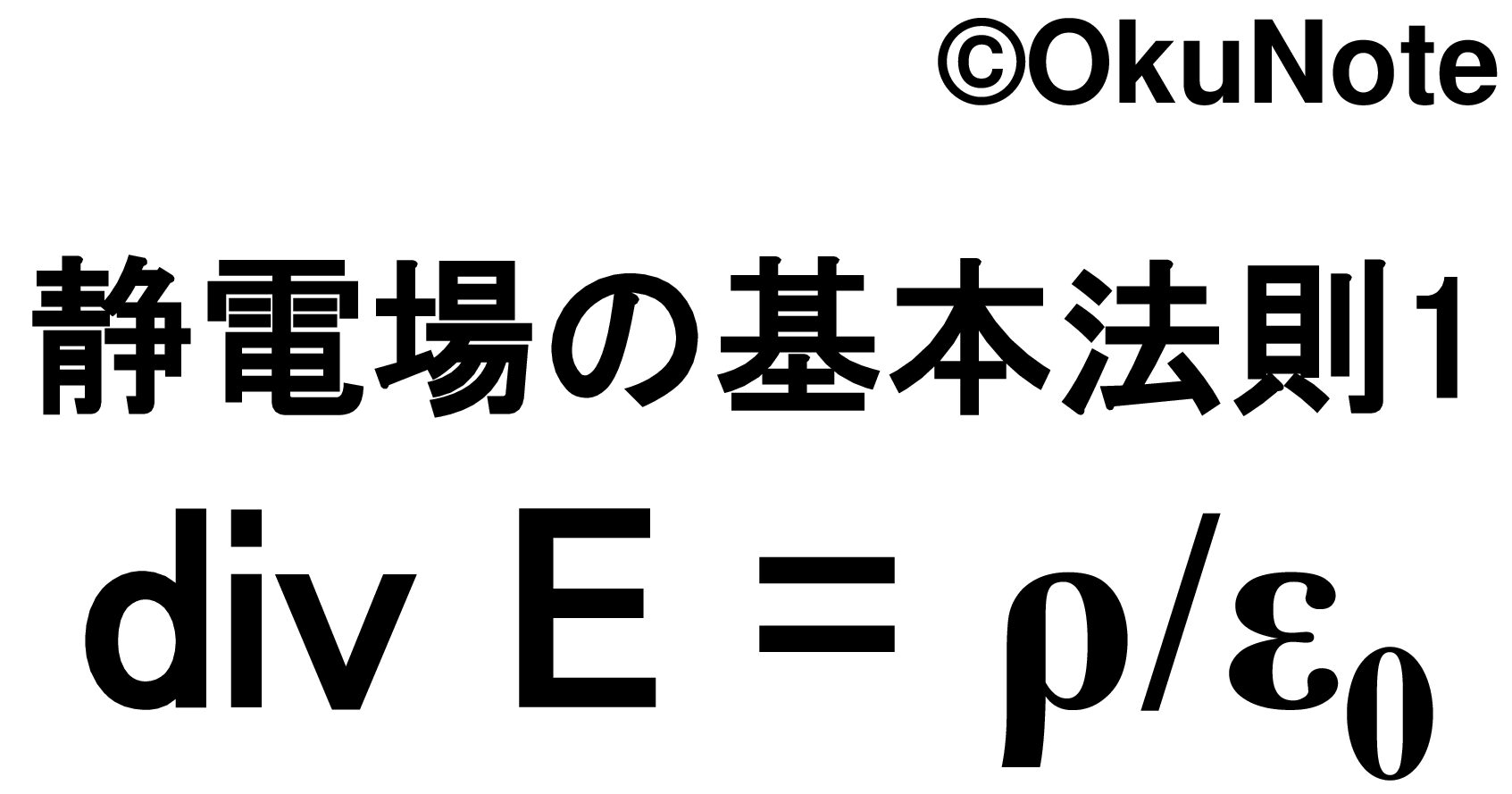


コメント