物理学において、波は力学、電磁気学、量子力学という様々な分野に頻繁に登場する。波の伝播方法には大きく分けて平面波と球面波という2つの種類がある。字からも推測可能なように、平面波は平面的に、球面波は球体に広がって伝播していく。この大雑把な理解のままでも勉強を進めることは可能だが、この機会にそれぞれの特徴を整理してみよう。
球面波は、近くにおいて波は完全に球面に広がっているが、波源から遠ざかっていくにつれて、この球面の曲率は次第に緩やかになっていき、最終的には平面波に近くなる。本記事では、このように球面波が平面波に近づいていく様子を数式に基づく展開と、Pythonによる数値シミュレーションによる可視化で説明する。
平面波
まずは平面波の定義をおさらいしよう。$z$方向に進む平面波は、
\begin{align}
\psi_\mathrm{plane}(z,t)=A \mathrm{e}^{i(kz-\omega t)}
\end{align}
と表せる。これは、位相速度は$v_\mathrm{p}=\omega/k$で$z$方向に進む波を表している。この表式には$x,y$の情報は含まないため、$z$が一定の面が等位相面となっている。このように等位相面が平面のまま伝播する波のことを平面波という。また、この単純な表式では、振幅$A$は定数であり伝播によって減衰しないことになっている。しかし、一般的には$A=A(z)$のように波の進行に従って振幅が変化する場合でも、等位相面が平面であれば平面波という場合も多い。
球面波
次に球面波については、
\begin{align}
\psi_\mathrm{sphere}(z,t)=\frac{A}{r} \mathrm{e}^{i(kr-\omega t)}
\end{align}
と表せる。ただし、$r=\sqrt{x^2+y^2+z^2}$であり、球座標の$r$である。球面波の場合には、球面上に波が広がるため、エネルギーが保存するとしても振幅は$1/r$で減衰することになる。そして、球面波における等位相面は、$r$が一定の球面である。このように等位相面が球面のまま伝播する波のことを球面波という。
球面波の平面波近似
以上のように平面波と球面波は、等位相面が異なるために差別化されることが分かった。しかし、伝播する球面波を十分遠くから見ると、球面の曲率が緩やかになっていき、いずれは平面とみなせるほどになり得る。これは、$r$について$z\gg x,y$として展開すると、
\begin{align}
r=\sqrt{x^2+y^2+z^2}=z+\frac{x^2+y^2}{2z}+\dots\simeq z+\frac{x^2+y^2}{2z}
\end{align}
と表せるため、球面波の表式は、
\begin{align}
\psi_\mathrm{sphere}(z,t)=\frac{A}{r} \mathrm{e}^{i(kr-\omega t)}\simeq\frac{A}{r} \mathrm{e}^{i(kz-\omega t)}\mathrm{e}^{i\frac{k(x^2+y^2)}{2z}}
\end{align}
と書ける。この表式において、最も変化の大きい$z$に着目すると、$\frac{A}{r}\mathrm{e}^{i(kz-\omega t)}$で表せる平面波成分が大きな寄与をもつ。最後の、$\mathrm{e}^{i\frac{k(x^2+y^2)}{2z}}$は開口などで気にしている$xy$平面上での広がりによる寄与であり、回折では重要な役割を果たすが、これらの寄与が無視できるほど遠方であれば平面波とみなせる。また、ここで平面波成分については、球面波由来の$1/r$の減衰が含まれている。ただし、平面波の定義でも述べたように、平面波において重要なのは等位相面であるから、等位相面が平面であれば平面波と呼ぶことにしている。
Fresnel距離
さて、十分遠方では球面波が平面波とみなせることは理解できたが、どれだけ離れたら平面波とみなせるか定量的な指針を与えるのがFresnel距離である。開口の大きさを$D$、波の波長を$\lambda$とするとき、
\begin{align}
z\gg \frac{D^2}{\lambda} =:z_\mathrm{F}
\end{align}
を満たすときに平面波近似できる。この下限を定めた$z_\mathrm{F}$のことをFresnel距離という。
これは、先ほどの平面波成分に対して曲率による補正項が無視できる基準を示すもので、以下のように導出できる。
まず、簡単のために、3次元の球面波のうち$y=0$で固定して$xz$平面上で考える。また、$t=0$における波は、
\begin{align}
\psi_\mathrm{sphere}(z,t)=\frac{A}{r} \mathrm{e}^{ikr}\simeq \frac{A}{z}\mathrm{e}^{ikz}\mathrm{e}^{i\frac{kx^2}{2z}}
\end{align}
と表せる。ここで、${e}^{ikz}\mathrm{e}^{i\frac{kx^2}{2z}}$が曲率補正項である。この位相、
\begin{align}
\Delta\phi(x)=\frac{kx^2}{2z}
\end{align}
に着目する。これは$2\pi$ radであれば、波として1周期分の変化になるため大きな影響を与える。そこで、経験的に1 radよりも十分小さければ、平面波に近似できると言える。このとき、開口$D$に対して、$x=D/2$で曲率補正項が無視できる条件は、
\begin{align}
\frac{kD^2}{8z}\ll 1 \Rightarrow z \gg \frac{kD^2}{8}=\frac{\pi D^2}{4\lambda}
\end{align}
となる。ただし、今は明確に1 radで上限を決める理由もなく、あくまでオーダーの議論のため係数は無視して、
\begin{align}
z\gg \frac{D^2}{\lambda} =: z_\mathrm{F}
\end{align}
によって下限値のFresnel距離$z_\mathrm{F}$を得る。
Pythonによる可視化
さて、最後にFresnel距離まで離れると球面波がどれだけ平面波に近づいているかを可視化する。
以下のグラフは、横軸$x$、縦軸$z$とし、球面波の等位相面を示した図である。ただし、波長は$\lambda=4.0$とし、開口は$D=10.0$とした。
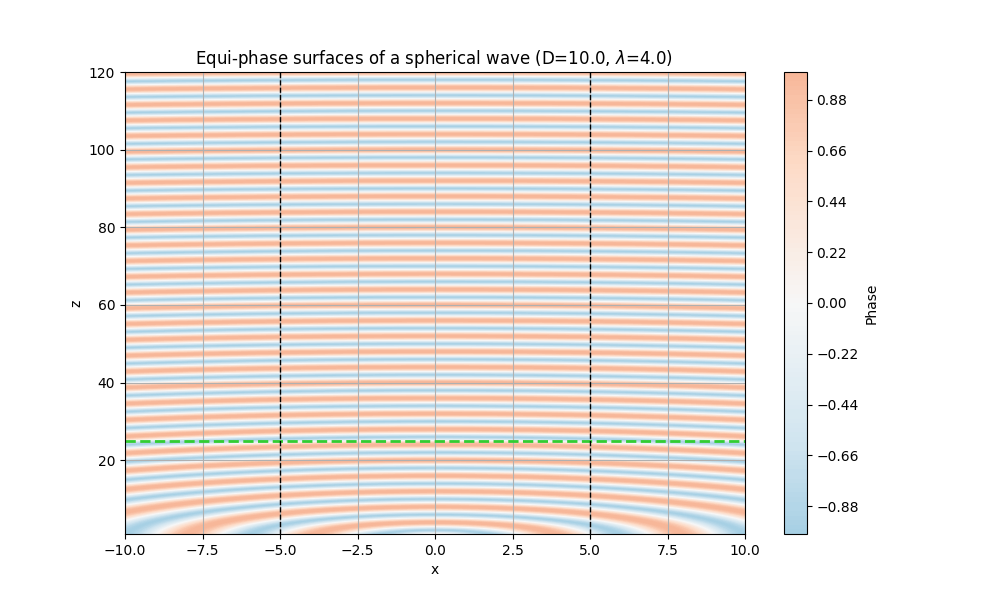
$x=z=0$を波源として、球面波が$xz$平面上で伝播していく様子が見える。開口$D=10.0$に対して、$x=\pm D/2=\pm 5.0$に囲まれる領域がいま考えている部分である。ここで、緑の破線で示した$z_\mathrm{F}=10^2/4=25$がFresnel距離である。つまり、黒の破線で囲まれた領域で、緑の破線まで離れれば十分平面波に近似できるということになる。たしかに、図を見てもその範囲では位相がほとんど変わらず一定とみなせることが分かる。
開口は$D=10.0$で固定したまま、$\lambda=10.0$とすると、下図のようになる。
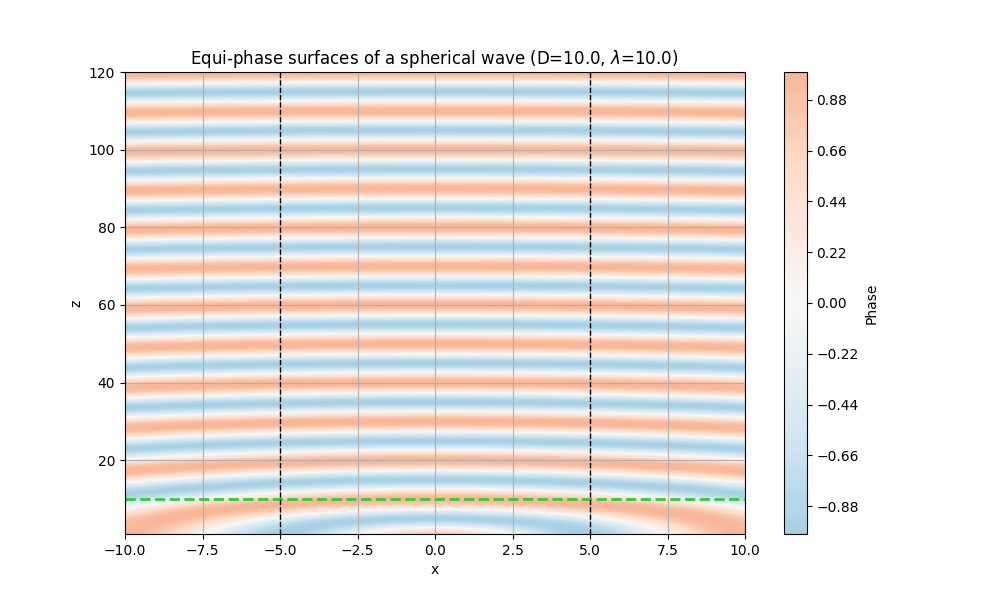
また、同じく開口は$D=10.0$で固定したまま、$\lambda=1.0$とすると、下図のようになる。
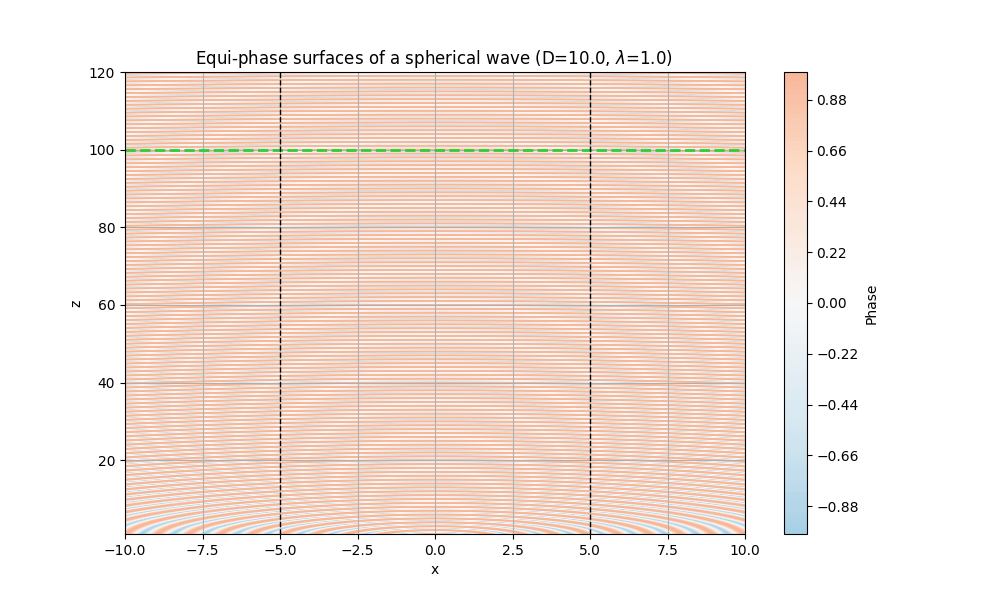
波長が小さいほど、横方向$x$に広がったときに位相の変化が起きやすいため、Fresnel距離が大きくなることが分かる。
まとめ
本稿においては、平面波と球面波の定義から球面波を平面波に近似して扱う条件を数式により導出し、Pythonによって視覚化した。
これにより、平面波近似というものが具体的にどういう意味なのか、波の形状もあわせて整理することができた。
難しくない内容という理由により教科書に詳しく解説してこない場合も少なくないが、このように整理しておくことで、波の振る舞いや近似条件の理解がより確かなものになると思う。
補足:使用したPythonのスクリプト
import numpy as np
import matplotlib.pyplot as plt
# Parameters
wavelength = 1.0 # Wavelength λ
k = 2 * np.pi / wavelength # Wavenumber k
D = 10.0 # Aperture size (used for Fresnel distance)
# Fresnel distance: estimate for far-field condition
fresnel_distance = D**2 / wavelength
# Observation plane (x-z plane) setup
x = np.linspace(-10, 10, 401)
z = np.linspace(1, 120, 2400)
z_min = np.min(z)
X, Z = np.meshgrid(x, z)
# Spherical wave at t = 0
R = np.sqrt(X**2 + Z**2)
wave = np.cos(k * R)
# Visualization (equi-phase contour plot)
plt.figure(figsize=(10, 6))
contour = plt.contourf(X, Z, wave, levels=100, cmap='RdBu_r', vmin=-3, vmax=3)
plt.colorbar(label='Phase')
plt.axhline(fresnel_distance, color='limegreen', linestyle='--', linewidth=2)
plt.axvline(D/2, color='black', linestyle='--', linewidth=1)
plt.axvline(-D/2, color='black', linestyle='--', linewidth=1)
plt.title(f'Equi-phase surfaces of a spherical wave (D={D}, $\lambda$={wavelength}) ')
plt.xlabel('x')
plt.ylabel('z')
plt.grid(True)
#plt.savefig('fresnel_distance_lam=1.png')
plt.show()

コメント