目的
前回の記事では、SOXL(Direxion デイリー半導体株ブル3倍ETF)を題材として、レバレッジETFの基本的な仕組みやリスク構造について紹介した。
レバレッジ(leverage)という言葉は、もともと英語で「てこの作用」を意味し、小さな力で大きなものを動かすことを表す。金融の世界においても、同様のイメージで用いられ、自己資金を元に他人資本(借入など)を利用して、投資の効率を高める仕組みを指す。たとえば信用取引、デリバティブ取引、さらには今回取り上げるレバレッジETFなどがその代表である。
この「レバレッジ3倍ETF」と呼ばれる商品は、元となる株価指数に対して日々の値動きの3倍のリターンを目指して設計されたファンドである。ここで注意が必要なのは、「指数の3倍になる」わけではなく、「指数の日々の変化率の3倍を目指す」という点である。これはつまり、元の指数のチャートを単純に3倍にスケールしたものとは、全く異なる値動きになることを意味する。
では、その「日々の変化率を3倍にしたもの」とは、実際にどのようなチャートを描くのだろうか?
そして、理論的な3倍レバレッジETFの値動きと、実際のETFであるSOXLのチャートはどの程度一致しているのだろうか?
本記事では、この疑問に答えるべく、Pythonを用いたシミュレーションとデータ可視化を行う。
今回の検証では、SOXLの基準とされるICE Semiconductor Index(ICE Semiconductor Index)が公開されていないため、代替として広く利用されているSOX指数(Philadelphia Semiconductor Index)を用いる。SOXはICE指数とは完全に一致はしないが、構成銘柄やパフォーマンスの傾向が非常に近く、参考指数として十分に機能する。
まずはSOXの実データをもとに、「日々の変化率を3倍に積み上げた理論的な3倍レバレッジのチャート」を再現し、それと実際のSOXLの値動きを比較する。さらに、両者の差分を可視化し、どの時期にどのような乖離が生じているのかを検証する。
Pythonでの実装と処理の流れ
今回のPythonスクリプトでは、以下の処理を統合的に実装した。実際に使用したコードは本記事の最後に掲載した。
データの読み込みと整形
実際のSOXおよびSOXLのチャートはExcel形式のデータに加工し、それをPythonで読み込んだ。ただし、レバレッジETFの原理に従い、毎日の値動きを計算する必要があるため日次のデータを用いた。Pythonのpadas.DataFrameに格納し、日付をdatetime型に変換して、日付順にソートした。
SOX指数からレバレッジ3倍の指数を再構成
レバレッジETFの原理に従い、SOX指数の日次リターンに対して毎日3倍となるように動作するSOX_3xと計算した。
sox_3x[t] = sox_3x[t-1] * (1 + 3 * 日次リターン)このような形で日次リターンに3倍を掛けて複利的に積み上げることで、理想的なレバレッジ3倍商品を再現した。
正規化(Normalize)
比較を容易にするため、すべての指数を今回用いたデータの開始点である2019年5月1日時点の値を100に統一してスケーリングした。ちなみに、コロナ禍前からの値動きを調べたかったため、この時期から現在までのデータを採用した。
Pythonで可視化した結果
まず、SOXのチャートとそのレバレッジ3倍を再現したSOX_3xのチャート、さらにSOXLのチャートをすべて重ねてグラフに示した。
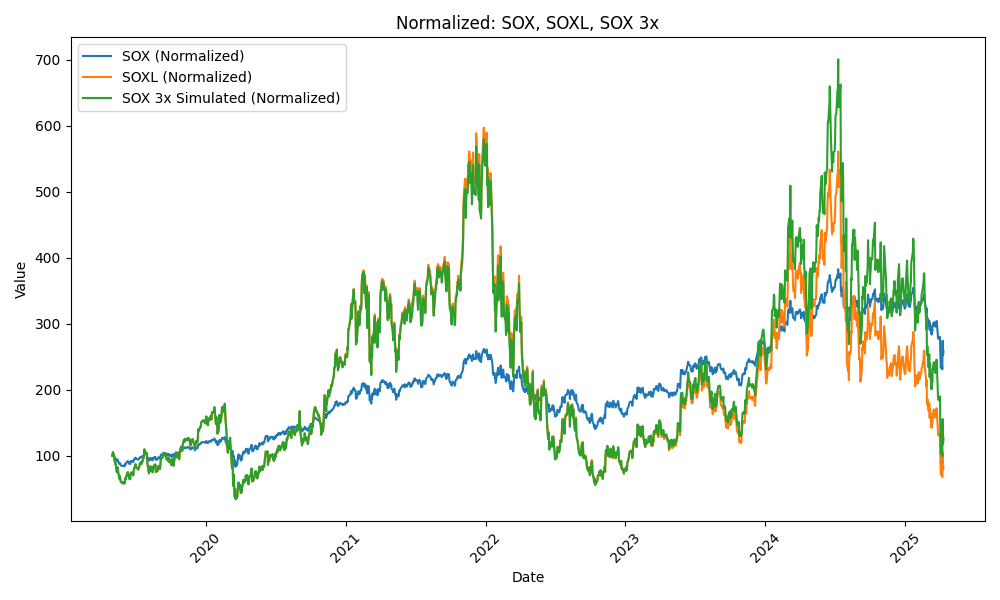
すでに述べたように、2019/5/1時点ですべての指数が100となるようにスケールを決めている。2020年のコロナショックや、その後の回復局面、さらに2024年の上昇局面などの同じトレンド内に限ってみれば元の指数の3倍に連動していることが確認できる。ところが、トレンドが反転し、上下するような局面になると減価が生じ、損失が発生する。実際にSOX指数をみると、2022年に一度200を超えて、その後少し下がりながら、2024年夏頃には300を超えるまでに再上昇している。一方で、SOX_3xを見ると2022年では約3倍に連動して600近くまで急騰しているものの、2024年夏の際には同じく600近くまでにしか上昇していない。また、SOXLは2023年までは非常によくSOX_3xに一致しており、目標通りの値動きをしていたことが分かる。しかし、2024年夏頃にはSOX_3xに及ばず、500ほどまでしか上昇しなかった。これにより、実際のSOXLでは2022での最高値を超えられなかったことが分かる (SOX指数では2024年夏に1.5倍まで成長していたのにも関わらず!)。
さて、次にSOX_3xとSOXLの乖離について詳しく見てみよう。次のグラフはSOX_3xとSOXLの差分をとったものである。
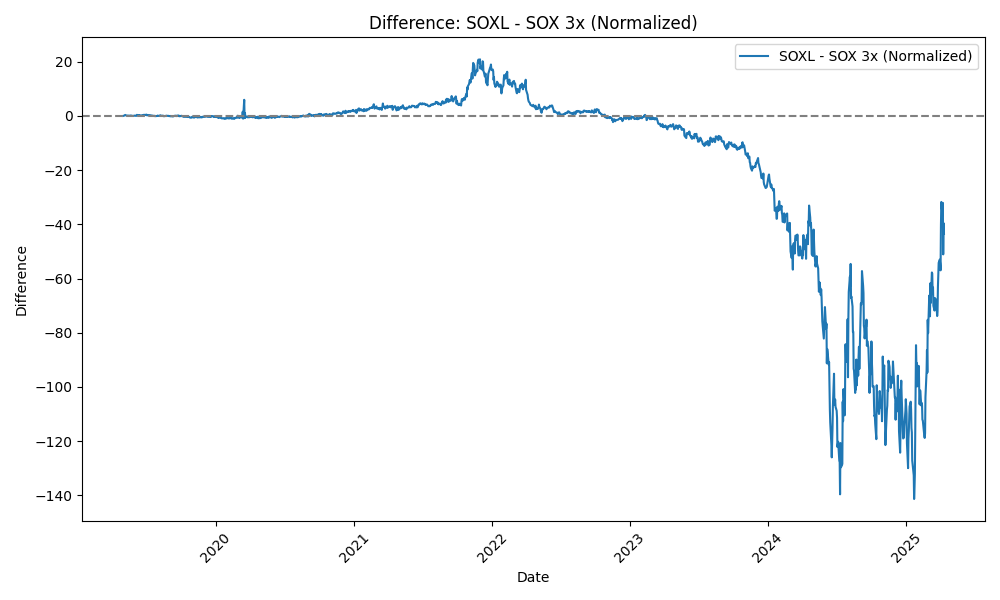
先ほども少し言及したように2023年まではほとんど乖離が見られずよく一致していたが、2024年からは大きくずれはじめたことが分かる。また、よく見ると2022年の急騰時にも実はSOXLが上振れしていたことが、このグラフから読み取れる。
考察:なぜ乖離が起きるのか?
2024年以降、SOXLは理論値を大きく下回るようになった。たしかにレバレッジは減価が発生するため、ボラティリティドラッグによって徐々に損失が蓄積しやすい。しかし、それはレバレッジの原理に基づくもののため、SOX_3xの再現に含まれる内容である。そこで、他に考えうる主な原因は以下の通りである。
- ボラティリティに応じたリバランスのタイミングの調整:
特に大きな上下があった日や相場が荒れているときに、運用会社がポジションの維持のためにリバランスを強化または抑制する可能性がある - 先物やスワップ等の実際の取引コストやスリッページ:
実際の3倍レバレッジを実現するには、先物やスワップといった金融派生商品の活用が必要であり、ここでの取引コスト、スプレッド、ロールオーバーによるコストが影響する。 - 配当や運用報酬等:
ETFには信託報酬(管理費用)が存在し、たとえばSOXLの場合は年率1%近い手数料が発生しており、これが日次でじわじわ価格に影響していく。長期では無視できない乖離要因。
以上、様々な要因によって乖離が生じ、それがさらに年次を追うごとにずれが蓄積されていくと考えられる。
それでは、年初の2024/1/2を基準に取り直したらどうなるだろうか?結果は以下の通りである。
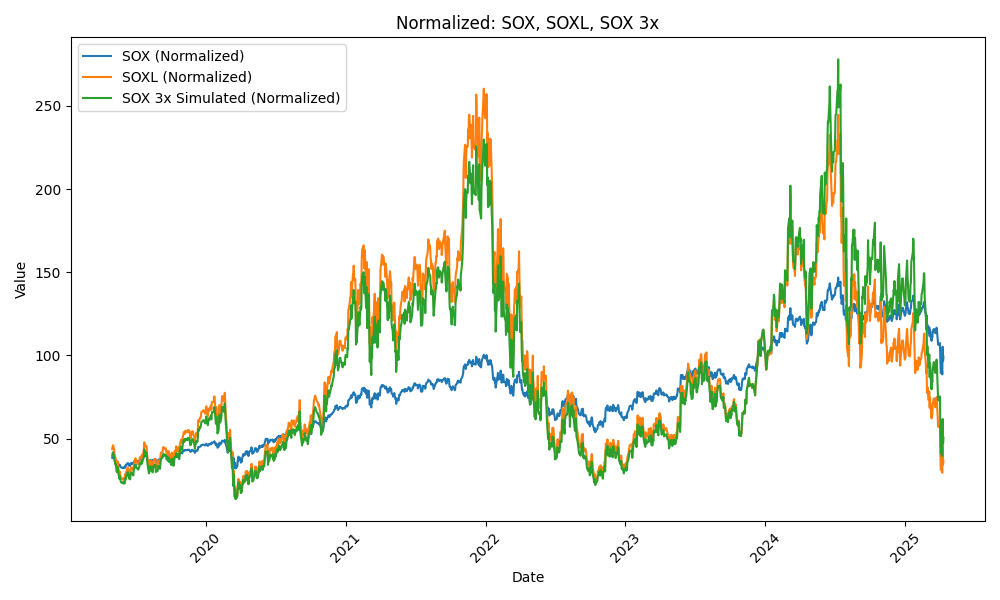
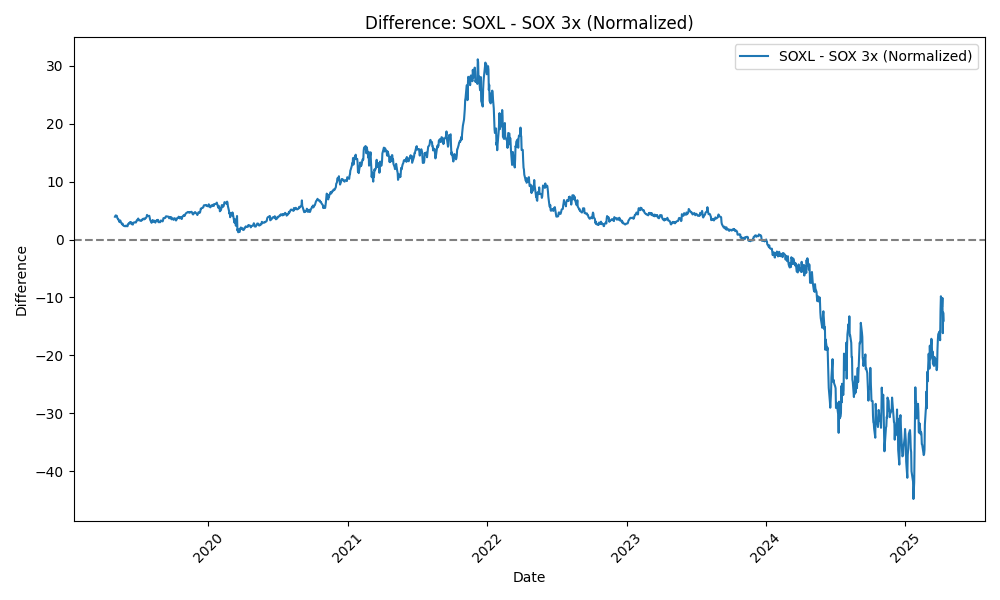
たしかに2024/1/2時点で一致するようにスケーリングされたことが分かるだろう。ところが、全体の振る舞いは変わらず、全体的にシフトしただけのように見える。つまり、指数のずれの大きさとしてはたしかに基準点によるが、乖離の根本的な原因ではない。
やはり、急激にトレンドが変化するような局面におけるリバランスによってこのような差異が生じると推測される。
結論とまとめ
本記事では、SOXLの実際の値動きと、SOXを基準として理論上の3倍指数をPythonでシミュレーションし、両者の乖離を可視化・分析した。その結果、以下のような知見が得られた。
- レバレッジ3倍を忠実に再現したチャートで、減価の仕組みが理解できた。
- 同トレンド内では元指数の3倍になるが、トレンド転換をまたぐと減価によりずれが生じる。
- 実際のSOXLと比較するとおおよそよく一致していたが、2024年夏の急騰時から乖離が大きくなった。
- リバランスなど、実運用上の要因が乖離を生むと考えられる
最後に、レバレッジETFは我々個人投資家が持つには様々なコストが生じる。レバレッジETFの購入時や売却時、さらに運用中の経費などで支払うことになる。これらのコストはSOXLのチャートには含まれないため、実際の手取りとしてはさらにこれらの費用を差し引いたものになることに注意されたい。
今回使用したPythonスクリプト
SOXおよびSOXLのチャートのデータは、SOX_chart.xlsxおよびSOXL_chart.xlsxというファイル名で保存し、このPythonスクリプトを同じフォルダにおいて実行すれば動作する。これら2つのエクセルファイルは、1列目に日付、2列目に指数のフォーマットで作成したものである。
なお、結果の考察する際に改造した分は含まない。
import pandas as pd
import matplotlib.pyplot as plt
from datetime import datetime
# ファイルの読み込み(事前に "SOXL_chart.xlsx" と "SOX_chart.xlsx" を同じディレクトリに置くこと)
soxl_df = pd.read_excel("SOXL_chart.xlsx")
sox_df = pd.read_excel("SOX_chart.xlsx")
# 日付を datetime 型に変換
soxl_df["Date"] = pd.to_datetime(soxl_df["Date"], format="%Y/%m/%d")
sox_df["Date"] = pd.to_datetime(sox_df["Date"], format="%Y/%m/%d")
# 日付で昇順にソート
soxl_df.sort_values("Date", inplace=True)
sox_df.sort_values("Date", inplace=True)
# 仮想3倍SOXの計算(日次リターンから累積、初期値を合わせる)
sox_df["Return"] = sox_df["Value"].pct_change().fillna(0)
sox_df["SOX_3x"] = (sox_df["Return"] * 3 + 1).cumprod() * sox_df["Value"].iloc[0]
# 2019/5/1 の値を基準にNormalize
base_date = datetime(2019, 5, 1)
base_sox = sox_df.loc[sox_df["Date"] == base_date, "Value"].values[0]
base_soxl = soxl_df.loc[soxl_df["Date"] == base_date, "Value"].values[0]
base_sox3x = sox_df.loc[sox_df["Date"] == base_date, "SOX_3x"].values[0]
# Normalize列の追加
sox_df["SOX_norm"] = sox_df["Value"] / base_sox * 100
sox_df["SOX_3x_norm"] = sox_df["SOX_3x"] / base_sox3x * 100
soxl_df["SOXL_norm"] = soxl_df["Value"] / base_soxl * 100
plt.figure(figsize=(10, 6))
plt.plot(sox_df["Date"], sox_df["SOX_norm"], label="SOX (Normalized)")
plt.plot(soxl_df["Date"], soxl_df["SOXL_norm"], label="SOXL (Normalized)")
plt.plot(sox_df["Date"], sox_df["SOX_3x_norm"], label="SOX 3x Simulated (Normalized)")
plt.legend()
plt.title("Normalized: SOX, SOXL, SOX 3x")
plt.xlabel("Date")
plt.ylabel("Value")
plt.xticks(rotation=45)
plt.tight_layout()
plt.savefig("norm_all.png")
plt.close()
# SOXL - SOX_3x 差分
diff = pd.merge(soxl_df[["Date", "Value"]], sox_df[["Date", "SOX_3x"]], on="Date", how="inner")
diff["Difference"] = diff["Value"] - diff["SOX_3x"]
plt.figure(figsize=(10, 6))
plt.plot(diff["Date"], diff["Difference"], label="SOXL - SOX 3x")
plt.axhline(0, color="gray", linestyle="--")
plt.legend()
plt.title("Difference: SOXL - SOX 3x")
plt.xlabel("Date")
plt.ylabel("Difference")
plt.xticks(rotation=45)
plt.tight_layout()
#plt.savefig("original_difference.png")
plt.close()
diff["SOXL_norm"] = soxl_df.set_index("Date").loc[diff["Date"], "SOXL_norm"].values
diff["SOX_3x_norm"] = sox_df.set_index("Date").loc[diff["Date"], "SOX_3x_norm"].values
diff["Norm_Diff"] = diff["SOXL_norm"] - diff["SOX_3x_norm"]
plt.figure(figsize=(10, 6))
plt.plot(diff["Date"], diff["Norm_Diff"], label="SOXL - SOX 3x (Normalized)")
plt.axhline(0, color="gray", linestyle="--")
plt.legend()
plt.title("Difference: SOXL - SOX 3x (Normalized)")
plt.xlabel("Date")
plt.ylabel("Difference")
plt.xticks(rotation=45)
plt.tight_layout()
plt.savefig("norm_difference.png")
plt.close()


コメント