Stokesの定理

電磁気学についてまとめたNoteの最新版：
https://okunotes.com/contents/Electromagnetism/Electromagnetism.pdf

Stokesの定理

この記事では、線積分を面積分と関係づけるStokesの定理について紹介する。この定理もベクトル解析において非常に重要な定理であり、電磁気学においても重要な役割を果たす。以前取り扱ったGaussの定理では、面積分を体積積分の関係性を与える定理であったのに対して、Stokesの定理は線積分と面積分の関係性を与える。

任意のベクトル場$\bm{E}$に対して、$S$は滑らかな境界$C$をもつ有界領域とし、$\bm{z}$を向きを保つ$C$の表示であるとして、以下が成り立つ。
\begin{align}
\oint_{C} \bm{E}\cdot \dd\bm{z} = \int_S \rot\bm{E}\cdot \dd\bm{S}.
\end{align}
ただし、$\text{rot}$とは
\begin{align}
\rot\bm{E}:= \nabla\times \bm{E}=\left(\del{E_z}{y}-\del{E_y}{z},\del{E_x}{z}-\del{E_z}{x},\del{E_y}{x}-\del{E_x}{y}\right)
\end{align}
で定義される回転(rotation)である。また、閉路の線積分である場合、明示的に$\oint$を使うことがある。ここで、回転を外積を用いて定義したが、ベクトル場の外積は次のような演算である。
\begin{align}
\bm{A}\times\bm{B}:=\left(A_yB_z-A_zB_y,AzB_x-A_xB_z,A_xB_y-A_yB_x\right).
\end{align}

証明

Gaussの定理と同様に、厳密な定義に基づいた証明はベクトル解析で行うが、簡単な証明を行う。
$xy$平面上の頂点$(x,y,0), (x+\Delta x,y,0), (x+\Delta x, y+\Delta y,0), (x,y+\Delta y,0)$から作られる長方形を考え、この座標の順番で結んだ経路を$C$とし、それに囲まれる平面を$S$とする。
経路$C$に沿ってベクトル$\bm{E}$を線積分する。このとき、4つの直線経路$r$ (right), $u$ (up), $l$ (left), $d$ (down)に分割する。

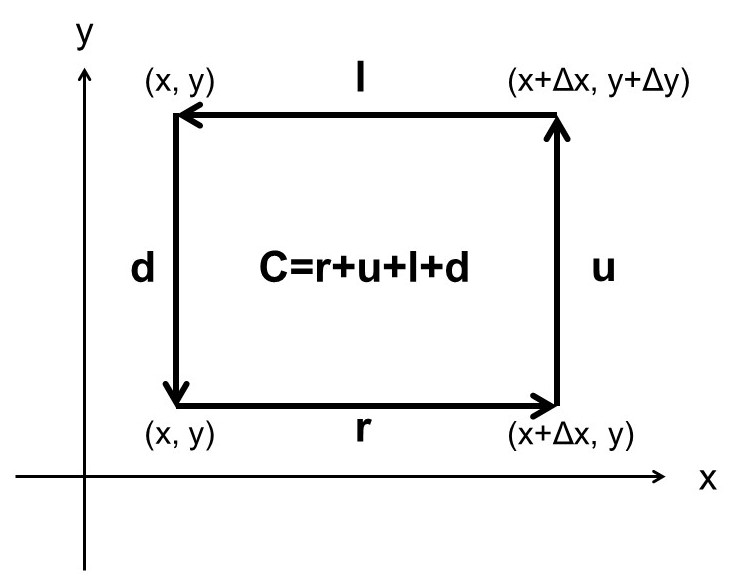
区間$r$では、$\bm{E}$の$x$成分が$E_x(x,y,0)\to E_x(x+\Delta x,y,0)$と変化するため、
\begin{align}
(区間rにおける\bm{E}のx成分)=E_x(x,y,0)+(\Delta x\text{の1次以上の項})
\end{align}
と書けるので、
\begin{align}
\int_r\bm{E}\cdot \dd\bm{z}=E_x(x,y,0)\Delta x+(\Delta x\text{の2次以上の項})
\end{align}
となる。
同様に、区間$u$では、$\bm{E}$の$y$成分が$E_y(x+\Delta x,y,0)\to E_y(x+\Delta x,y+\Delta y,0)$と変化するため、
\begin{align}
(区間uにおける\bm{E}のy成分)=E_y(x+\Delta x,y,0)+(\Delta y\text{の1次以上の項})
\end{align}
と書けるので、
\begin{align}
\int_u\bm{E}\cdot \dd\bm{z}=E_x(x+\Delta x,y,0)\Delta y+(\Delta y\text{の2次以上の項})
\end{align}
となる。また区間$l$では、$\bm{E}$の$x$成分が$E_x(x+\Delta x,y+\Delta y,0)\to E_x(x,y+\Delta y,0)$と変化するため、
\begin{align}
(区間lにおける\bm{E}のx成分)=E_y(x,y+\Delta y,0)+(\Delta x\text{の1次以上の項})
\end{align}
と書けるので、
\begin{align}
\int_l\bm{E}\cdot \dd\bm{z}=E_x(x,y+\Delta y,0)\Delta x+(\Delta x\text{の2次以上の項})
\end{align}
となる。最後に区間$d$では、$\bm{E}$の$y$成分が$E_y(x,y+\Delta y,0)\to E_x(x,y,0)$と変化するため、
\begin{align}
(区間dにおける\bm{E}のy成分)=E_y(x,y,0)+(\Delta y\text{の1次以上の項})
\end{align}
と書けるので、
\begin{align}
\int_d\bm{E}\cdot \dd\bm{z}=E_x(x,y,0)\Delta y+(\Delta y\text{の2次以上の項})
\end{align}
となる。

よって、閉路$C=r+u+l+d$における線積分は、微小量$\Delta x, \Delta y$の2次以上を無視すると、
\begin{align}
\oint_C \bm{E}(x,y,0)\cdot \dd \bm{z}&=E_x(x,y,0)\Delta x+E_y(x+\Delta x,y,0)\Delta y\nonumber\\
&\quad+E_x(x,y+\Delta y,0)(-\Delta x)+E_y(x,y,0)(-\Delta y)\nonumber\\
&=\frac{E_y(x+\Delta x,y,0)-E_y(x,y,0)}{\Delta x}\Delta x\Delta y\nonumber\\
&\quad-\frac{E_x(x,y+\Delta y,0)-E_y(x,y,0)}{\Delta y}\Delta x\Delta y\nonumber\\
&=\left(\del{E_y(x,y,0)}{x}-\del{E_x(x,y,0)}{y}\right)\Delta x\Delta y\nonumber\\
&=\left(\rot\bm{E}(x,y,0)\right)_z \Delta x\Delta y=\int_S \rot\bm{E}\cdot \dd\bm{S}
\end{align}
と書ける。ただし、$\bm{S}$の向きは境界線$C$の右ねじの方向にとる。

また、
\begin{align}
\left(\rot\bm{E}(x,y,0)\right)_z=\mathrm{lim}_{\Delta x,\Delta y\to0}\frac{1}{\Delta x\Delta y}\oint_C \bm{E}(x,y,0)\cdot \dd \bm{z}
\end{align}
であり、ある$z$における平面$\Delta x\Delta y\to0$の境界線を1周回転するベクトル場$\bm{E}$の量が$\rot\bm{E}$の$z$成分を表していると解釈できる。このことから、$\text{rot}$は回転という。

以上の議論は、$z=0$に固定したものであったが、任意にとった平面でも全く同様である。以上の証明は微小な長方形に限ったStokesの定理であった。一般の閉曲線に対しても、非常に細かく長方形で閉曲線内の平面を区切っていくと各長方形では同様にStokesの定理が成り立つ。すると、隣合う境界では接線ベクトルが反平行になるため、相殺され結果として閉曲線上の効果のみが残る。すなわち、一般の閉曲線に対しても、Stokesの定理が成り立つことが分かる。

よって、
\begin{align}
\oint_{C} \bm{E}\cdot \dd\bm{z} = \int_S \rot\bm{E}\cdot \dd\bm{S}
\end{align}
となり、表式を得る。