Gaussの定理
この記事では、面積分を体積積分と関係づけるGaussの定理について紹介する。ベクトル解析において非常に重要で基本的なこの定理は、特に電磁気学において大活躍する。この記事では扱わないが、Gaussの法則の面積分を体積積分に変えることによって、(静)電場の基本法則の1つ目が得られる。
任意のベクトル場$\bm{E}$に対して、$V$は滑らかな境界(表面)$S$をもつ有界領域とすると以下が成り立つ。
\begin{align}
\int_{S} \bm{E}\cdot \bm{n}\, \dd S = \int_V \mathrm{div}\,\bm{E}\, \dd^3 x
\end{align}
ただし、$\text{div}$とは
\begin{align}
\mathrm{div}\,\bm{E}:= \nabla\cdot \bm{E}=\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}
\end{align}
で定義される発散(divergence)である。
証明
厳密な定義に基づいた証明はベクトル解析で行うが、簡単な証明をここで行う。この証明を追えば、発散のイメージもできるようになるはずである。また、この証明法はベクトル解析にて行うものと基本的には同一である。
$z$座標が$z$である平面上の頂点$(x,y,z), (x+\Delta x,y,z), (x,y+\Delta y,z), (x+\Delta x, y+\Delta y,z)$から作られる長方形を$z$方向に$\Delta z$だけ押し出してつくった微小な直方体を考える。
この直方体の表面積を$S$、それに囲まれる内部の領域を$V$とする。
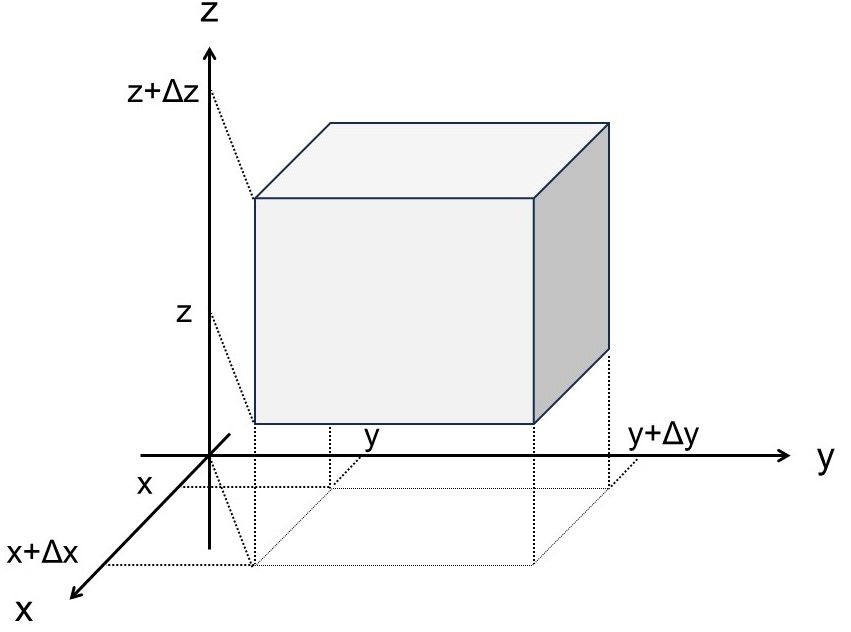
直方体は6つの面があるが、$x=x+\Delta x$である面について考えると、
\begin{align}
\int_{x+\Delta x}\bm{E}\cdot\bm{n}\, \dd S= E_x(x+\Delta x,y,z)\Delta y\Delta z
\end{align}
と書ける。同様に、$x+\Delta x$の面については、
\begin{align}
\int_{x}\bm{E}\cdot\bm{n}\dd S= -E_x(x,y,z)\Delta y\Delta z
\end{align}
と書ける。
これらを合わせると、次のように表せる。
\begin{align}
\int_{x\cup (x+\Delta x)}\bm{E}\cdot\bm{n}\, \dd S= \frac{E_x(x+\Delta x,y,z)-E_x(x,y,z)}{\Delta x}\Delta x\Delta y\Delta z=\frac{\partial E_x}{\partial x}\Delta^3 x
\end{align}
同様にして、
\begin{align}
\int_{y\cup (y+\Delta y)}\bm{E}\cdot\bm{n}\, \dd S&= \frac{E_y(x,y+\Delta,z)-E_x(x,y,z)}{\Delta y}\Delta x\Delta y\Delta z=\frac{\partial E_y}{\partial y}\Delta^3 x\\
\int_{z\cup (z+\Delta z)}\bm{E}\cdot\bm{n}\, \dd S&= \frac{E_x(x,y,z+\Delta z)-E_x(x,y,z)}{\Delta x}\Delta x\Delta y\Delta z=\frac{\partial E_z}{\partial z}\Delta^3 x
\end{align}
と書ける。
以上の結果を合わせると、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n}\, \dd S= \int_V \left(\frac{\partial E_x}{\partial x}+\frac{\partial E_y}{\partial y}+\frac{\partial E_z}{\partial z}\right)\, \dd^3 x
= \int_V \mathrm{div}\,\bm{E}\, \dd^3 x
\end{align}
となり、Gaussの定理が成り立つことが示せる。
一般の領域に対しても、非常に細かく直方体で空間を区切っていくと各直方体では同様にGaussの定理が成り立つ。すると、隣合う面どうしでは法線ベクトルが反平行になるため、相殺され結果として領域の外側の表面の効果のみが残る。すなわち、一般の領域に対しても、滑らかに接続された境界に囲まれる領域に対してはGaussの定理が成り立つことが分かる。
また、
\begin{align}
\mathrm{div}\,\bm{E}(\bm{x})=\lim_{\Delta^3 x\to 0}\frac{1}{\Delta^3 x}\int_S \bm{E}\cdot\bm{n}\, \dd S
\end{align}
であり、微小な箱$\Delta^3x\to 0$の中から「湧き出る」ベクトル場$\bm{E}$の量を表していると解釈できる。このことから、$\text{div}$は発散や湧き出しという。


コメント