ここまでは実験結果に基づいて得られたCoulombの法則を利用していた。この法則があれば、電荷分布を与えられたときの電場や、それによって電荷に働く力を計算することができる。次は、そこから理論を少し飛躍させることでGaussの法則を議論する。
逆2乗則
Coulombの法則によると、力の大きさは距離$r$に対して$1/r^2$に比例する。これは実験結果によって、$1/r^{2+\delta}$としたときに現在の精度で$|\delta|<2\times 10^{-9}$であることが保証されている。
ここで論理を少し飛躍させて、たまたま距離の約2乗に反比例するのではなく、逆2乗則、すなわち厳密に距離の2乗に反比例すると考えることでGaussの法則を見い出せる。ここは論理の飛躍があることだが、物理学においてこれが正しいことを実証するには、この仮説から導き出された結論が実験結果と矛盾しないことを示せばよい。現代の物理学においても、この点において矛盾が見られていないため、どうやら正しいようである。
逆2乗則とは、空間が3次元であることを反映している。3次元空間のある点から等方的に放射されるエネルギーや力が距離$r$に応じてどのように広がるかを考えてみよう。等方的であれば、すべて球状に広がるだろう。そして、この球の表面積は$4\pi r^2$であり、距離$r$の2乗に比例する。このとき、このエネルギーや力は広がる球の表面に均等に分布されるわけであるから、単位面積あたりの強度は$1/(4\pi r^2)$であり、距離$r$の2乗に反比例する。この性質が逆2乗則である。すなわち、3次元空間上に等方的に放射されると考えるなら、強度は距離$r$の2乗に反比例すると考えられる。
そこで、電場についても同様であると仮定してみる。いくつかのケースを想定する。
球の内部に電荷があるとき
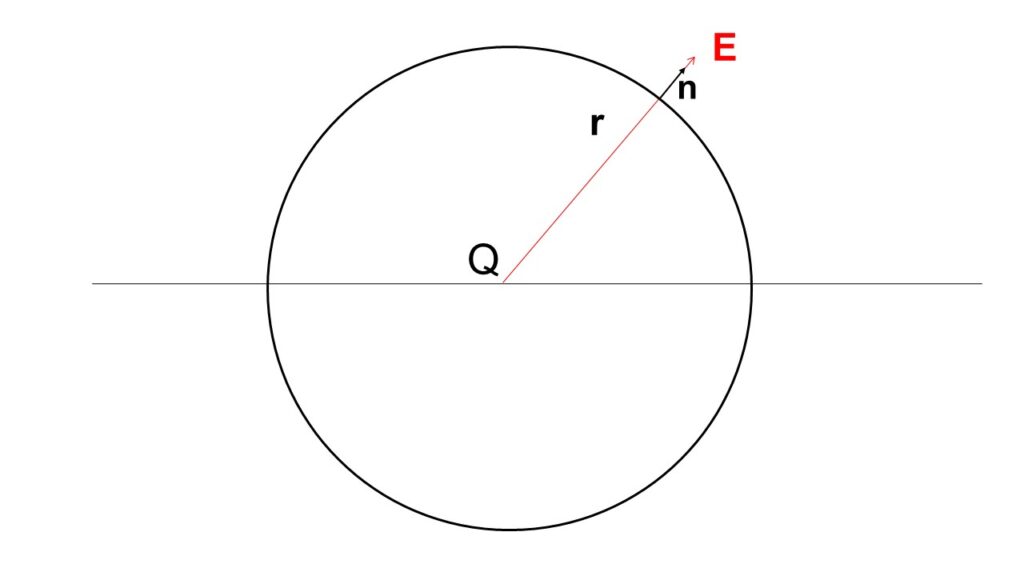
図のように電荷$Q$をもつ点電荷を位置$\bm{z}$におき、そこを中心とした半径$r:=|\bm{x}-\bm{z}|$の球面$S$を考える。このとき、球面$S$における電場$\bm{E}$と、球面$S$に直交する外向きの法線ベクトル$\bm{n}$は、
\begin{align}
\bm{E}(\bm{x})=\frac{Q}{4\pi\varepsilon_0}\frac{\bm{x}-\bm{z}}{|\bm{x}-\bm{z}|^3},\ \ \ \ \bm{n}(\bm{x})=\frac{\bm{x}-\bm{z}}{|\bm{x}-\bm{z}|}
\end{align}
と書ける。この法線ベクトルがなぜ必要かというと、これから球面$S$上で電場を面積分したいからである。
\begin{align}
\int_{S} \bm{E}\cdot \dd \bm{S} = \int_{S} \bm{E}\cdot \bm{n} \dd S=\frac{Q}{4\pi \varepsilon_0}\frac{1}{r^2}\cdot 4\pi r^2=\frac{Q}{\varepsilon_0}
\end{align}
球の中心にある電荷$Q$を真空の誘電率$\varepsilon_0$で割った量が残った。
球の外部に電荷があるとき
それでは、球面$S$を電荷の外にとったときはどうなるだろうか。
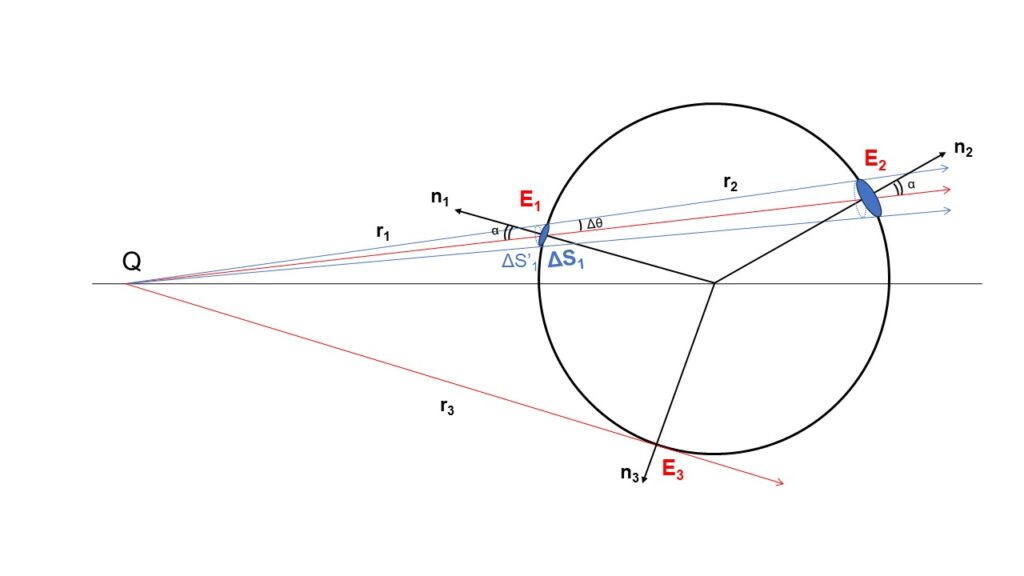
点電荷$Q$とは離れたところに中心をもち、かつその球内に電荷を含まない場合を考える。
このとき、球を貫く電場は$\bm{r}_3$のように接線となる場合を除き、球面を2度貫く。外側から内側へ貫く位置を$\bm{r}_1$、その後内側から外側へ貫く位置を$\bm{r}_2$とする。このときに貫く微小な球面$\Delta S’_1$、$\Delta S’_2$はそれぞれ、$\bm{r}_{1,2}$から$\Delta\theta$の角度をもって$2\pi$回転して作られる球面とする。この球面の面積は、$\bm{r}_{1,2}$を$z$軸と見立てて球面座標系を用いれば求めることができる。
\begin{align}
\Delta S’_1 &= \int_{\theta=0}^{\Delta\theta} \int_{\phi=0}^{2\pi} r_1^2\sin\theta\ \dd\theta\dd\phi=2\pi r_1^2(1-\cos\Delta\theta)\\
\Delta S’_2 &= \int_{\theta=0}^{\Delta\theta} \int_{\phi=0}^{2\pi} r_2^2\sin\theta\ \dd\theta\dd\phi=2\pi r_2^2(1-\cos\Delta\theta)
\end{align}
ただし、これは点電荷$Q$の位置を中心とした球の表面積の一部であって、いま考えている球面$S$の一部ではない。それぞれの球面が角度$\alpha$だけ傾いている、またはそれぞれの法線ベクトルのなす角が$\alpha$であるともいえる。すなわち、
\begin{align}
\Delta S_1 &= \Delta S’_1\cos \alpha = 2\pi r_1^2(1-\cos\Delta\theta)\cos \alpha\\
\Delta S_2 &= \Delta S’_2\cos \alpha = 2\pi r_2^2(1-\cos\Delta\theta)\cos \alpha
\end{align}
である。これらの面における電場の面積分を考えると、
\begin{align}
\int_{\Delta S_1} \bm{E}_1\cdot \bm{n}_1 \dd S& = |\bm{E}_1||\bm{n}_1|\cos (\pi-\alpha) \Delta S_1\nonumber\\
&=-\frac{Q}{4\pi \varepsilon_0}\frac{1}{r_1^2}\cdot \cos \alpha\cdot 2\pi r_1^2(1-\cos\Delta\theta)\cos \alpha\\
\int_{\Delta S_2} \bm{E}_2\cdot \bm{n}_2 \dd S& = |\bm{E}_2||\bm{n}_2|\cos \alpha \Delta S_1\nonumber\\
&=+\frac{Q}{4\pi \varepsilon_0}\frac{1}{r_2^2}\cdot \cos \alpha\cdot 2\pi r_2^2(1-\cos\Delta\theta)\cos \alpha
\end{align}
と書ける。やや長い式ではあるが、これら2式の違いは符号だけである。$r_1$と$r_2$については、クーロンの法則から生じる電場の$1/r^2$と、球の表面積により生じる$r^2$が互いに相殺される。したがって、
\begin{align}
\int_{\Delta S_1+\Delta S_2} \bm{E}\cdot \bm{n} \dd S=\int_{\Delta S_1} \bm{E}_1\cdot \bm{n}_1 \dd S+\int_{\Delta S_2} \bm{E}_2\cdot \bm{n}_2 \dd S=0
\end{align}
を得る。同様に、角度$\alpha$が異なる球面を考えても球面Sの入口と出口で、電場の面積分の結果は相殺されることになる。また、以上の内容は点電荷$Q$と球の中心を結ぶ軸に対して回転対称な系での議論のため、任意の角度で紙面方向に傾いた電場を考えても図全体を回転させることで同様の議論ができる。
さらに、はじめに述べたように$\bm{r}_3$のように1点しか接点をもたないものを考えると、これは球に正接しているため、$\bm{E}_3\cdot \bm{n}_3=0$となるからこれもまた電場の面積分はゼロとなる。
したがって、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S=0
\end{align}
を得る。
ここまでの結果を合わせると、球面$S$の場合、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S=
\begin{cases}
\frac{Q}{\varepsilon_0} & (Sの中心に点電荷Qがあるとき)\\
0 & (Sの外部に点電荷Qがあるとき)
\end{cases}
\end{align}
であることが分かった。
任意の閉曲面の内部に電荷があるとき
さらに、球面を一般の閉曲面に拡張してみる。
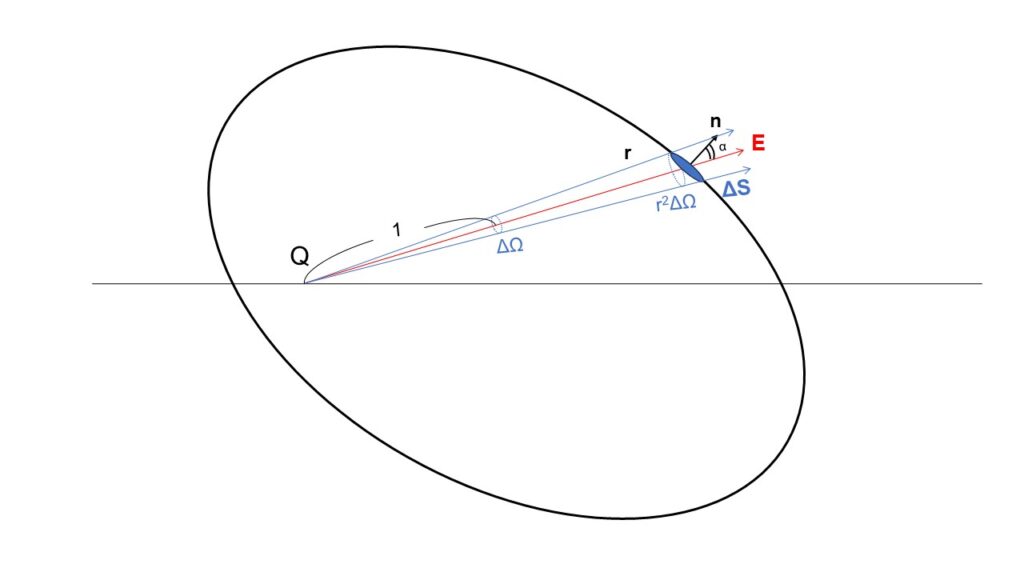
こうなると簡単に表面積を表すことができなくなる。そこで、立体角というものを用いて表す。これは2次元の場合の角度ラジアンが、単位半径の円弧の長さで定義されるのを、3次元に拡張したものである。立体角の単位はステラジアンといい無次元量であり、単位球の表面積の大きさで定義する。角度は全周で$2\pi$であるが、立体角は全球で$4\pi$である。
さて、ここで上図で点電荷$Q$を囲む閉曲面$S$を考える。
議論の内容は、すでに上で行ったことと同じである。
まずは、微小に区切られた面積$\Delta S$を求めたい。そのために、これを立体角$\Delta \Omega$と関係づける。面$\Delta S$を、$\bm{r}$ベクトルと直交するように角度$\alpha$だけ傾けて、さらに点電荷$Q$から距離$1$のところまで縮小して移動させると$\Delta \Omega$となる。距離$r$だけ離れた位置では、距離と面積の関係から$r^2\Delta \Omega$に拡大される。一方で、これは先ほど途中で角度$\alpha$だけ傾けたときの面積でもあったから、
\begin{align}
r^2\Delta \Omega = \Delta S\cos \alpha
\end{align}
の関係がある。
それでは、この閉曲面$S$における電場の面積分を計算しよう。上の関係はどの微小曲面$\dd S\ (\Delta S\to 0)$でも成り立つから、
\begin{align}
\bm{E}\cdot \bm{n}\dd S = \frac{Q}{4\pi \varepsilon_0 r^2}\cos \alpha \dd S = \frac{Q}{4\pi \varepsilon_0}\dd\Omega
\end{align}
である。よって、
\begin{align}
\int_S \bm{E}\cdot \bm{n}\dd S =\frac{Q}{4\pi \varepsilon_0}\int\dd\Omega= \frac{Q}{\varepsilon_0}
\end{align}
となる。
つまり、閉曲面$S$は球面でなくても、内部に点電荷$Q$があるときの電場の面積分の結果は$Q/\varepsilon_0$となることが分かった。これは同時に、点電荷が中心ではなく内部のどの位置に存在してもよいことを意味している。
任意の閉曲面の外部に電荷があるとき
それでは、外部に点電荷があるときはやはり電場の面積分の結果はゼロとなるだろうか。これはほぼ同じ議論になるため省略するが、やはりゼロになるのである。球面で考えていたときに、$\Delta S_1$と$\Delta S_2$が出てきたが、実は
\begin{align}
\Delta S_1 &= r_1^2 \Delta \Omega \\
\Delta S_2 &= r_2^2 \Delta \Omega
\end{align}
という関係であり、球面の場合には$\Delta \Omega$の具体的な表式が、
\begin{align}
\Delta \Omega =2\pi (1-\cos\Delta\theta)\cos \alpha
\end{align}
と与えられていたのである。そのため、それ以降の議論は全く同様であり、
\begin{align}
\int_{\Delta S_1+\Delta S_2} \bm{E}\cdot \bm{n} \dd S=\int_{\Delta S_1} \bm{E}_1\cdot \bm{n}_1 \dd S+\int_{\Delta S_2} \bm{E}_2\cdot \bm{n}_2 \dd S=0
\end{align}
となる。
任意の閉曲面を考えるため、閉曲面に入って出るだけとは限らない。閉曲面に対して、複数回出入りすることもあり得る。この場合も、入る回数と出る回数は同じため、それぞれで相殺されて最終的に電場の面積分はゼロとなるのである。また、閉曲面に対して正接する場合には、やはり電場ベクトルと法線ベクトルが直交するためゼロである。
以上の考察から、閉曲面$S$は球面でなくても、外部に点電荷$Q$があるときの電場の面積分の結果は$0$となることが分かった。
ここまでの結果を合わせると、任意の閉曲面$S$に対して、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S=
\begin{cases}
\frac{Q}{\varepsilon_0} & (Sの内部に点電荷Qがあるとき)\\
0 & (Sの外部に点電荷Qがあるとき)
\end{cases}
\end{align}
であることが分かった。
さらに一般化
ここで満足してはいけない。まだ拡張できるのである。点電荷の個数を増やし、さらに連続した電荷分布を考えてもよい。この場合の一般化は電場の重ね合わせの原理により容易である。
つまり、閉曲面$S$に対して、その内部に点電荷が$Q_1,Q_2,\dots,Q_n$、外部に$Q_{n+1}, \dots, Q_m$と用意したとき、
\begin{align}
\bm{E}=\bm{E}_1+\bm{E}_2+\dots+\bm{E}_n+\bm{E}_{n+1}+\dots+\bm{E}_m
\end{align}
となるから、
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S&=\int_{S} (\bm{E}_1+\bm{E}_2+\dots+\bm{E}_n+\bm{E}_{n+1}+\dots+\bm{E}_m)\cdot \bm{n} \dd S\nonumber\\&=\frac{Q_1+Q_2+\dots+Q_n}{\varepsilon_0}
\end{align}
また、同様に連続な電荷分布$\rho(\bm{x})$を考えた場合も、閉曲面$S$の内部領域$V$に含まれる総電荷$\int_V \rho(\bm{x})\dd^3 x$だけが残る。
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S=\frac{1}{\varepsilon_0}\int_V \rho(\bm{x})\dd^3 x
\end{align}
以上の考察によって得られた結果がGaussの法則である。
\begin{align}
\int_{S} \bm{E}\cdot \bm{n} \dd S=\frac{(\text{閉曲面S内部の総電荷})}{\varepsilon_0}
\end{align}
Gaussの法則のポイントは、はじめに述べたようにCoulombの法則は逆2乗則に従うものだと論理を飛躍させたことである。導出の過程でも重要であったのは、Coulombの法則により生じる$|\bm{E}|\propto 1/r^2$と、微小曲面積$\dd S =r^2\dd\Omega$が、面積分するときに相殺されて$r$に対する依存性が残らないことだった。ここが厳密に相殺されるのはCoulombの法則において、$|\bm{E}|\propto 1/r^{2+\delta}$で$\delta =0$としているからである。実験結果では$|\delta|<2\times 10^{-9}$でありすでに十分小さいが、Gaussの法則が発見された当時はまだ誤差も大きかったため、誤差を無視したのではなく$\delta$が厳密にゼロであると仮定したことで得られた法則である。これが我々の現実世界において成立することは、このあとGaussの法則に基づいて得られた結論が実験結果と何1つ矛盾しないことによって確かめられる。



コメント