電磁気学についてまとめたNoteの最新版：
https://okunotes.com/contents/Electromagnetism/Electromagnetism.pdf
電場
Coulombの法則を用いた解法
まずはCoulombの法則を用いて、無限長一様帯電棒のつくる電場を求める。
【問題】
$z$軸上にある細い針金に一様に帯電させ、単位長さあたりの電荷の線密度を$\lambda$とする。このとき、$z$軸から距離$R$だけ離れた位置$P$の電場を求めよ。
位置$-z’$の微小線長$\dd z’$がもつ電荷は$\lambda \dd z’$である。
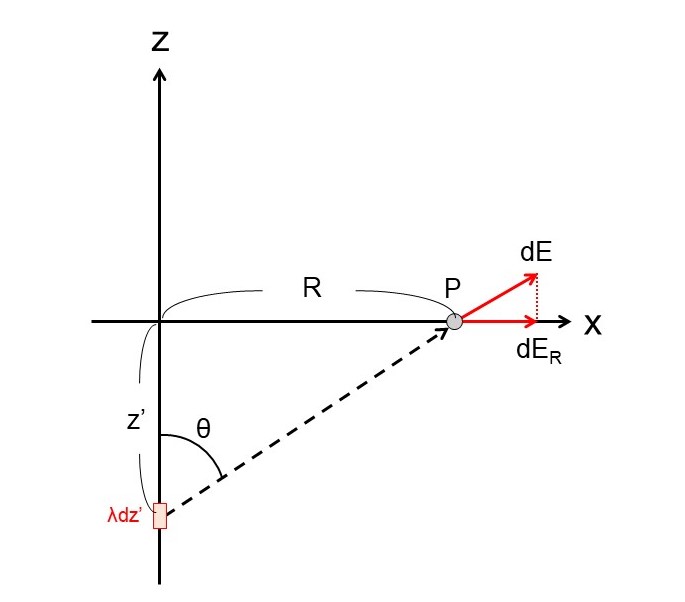
このとき、点$P$につくる電場の大きさは、上図より、
\begin{align}
|\dd \bm{E}|= \frac{1}{4\pi \varepsilon_0} \frac{\lambda \dd z’}{R^2+z’^2}
\end{align}
と表せる。
これを$z’$について$-\infty$から$\infty$まで積分すればいいのだが、系の対称性から積分して得られる電場は円筒座標系$(R,\phi,z)$において、$R$方向の成分しか持たない。なぜなら、$\phi$方向と$z$方向に関しては問題設定上、特定の位置を特徴づけることができないため電場は$\phi$依存性および$z$依存性は持てないからである。つまり$E(R)=\int_{z’=-\infty}^{z’=\infty} \dd E_R$である。
ここで、図中で定義される角度$\theta$を用いると、
\begin{align}
\dd E_R = |\dd \bm{E}|\sin\theta
\end{align}
であり、$\tan\theta = R/z’$より、$z’=R/\tan\theta$であり、
\begin{align}
\dd z’ = -\frac{R}{\tan^2\theta}\frac{\dd\theta}{\cos^2\theta}=-\frac{R}{\sin^2\theta}\dd\theta
\end{align}
である。
よって、$z’$の積分を$\theta$の積分に置き換えることで計算が進み、
\begin{align}
E(R)&=\int_{z’=-\infty}^{z’=\infty} \dd E_R\nonumber\\
&=\frac{\lambda}{4\pi \varepsilon_0}\int_0^\pi \frac{- \frac{R}{\sin^2\theta}\sin\theta}{R^2(1+\frac{1}{\tan^2\theta})}\dd\theta\nonumber\\
&=\frac{\lambda}{4\pi \varepsilon_0 R}\int_0^\pi \sin\theta\dd \theta = \frac{\lambda}{2\pi \varepsilon_0 R}
\end{align}
を得る。
したがって、無限長一様帯電棒がその周りにつくりだす電場の大きさは、
\begin{align}
E(R) = \frac{\lambda}{2\pi \varepsilon_0 R}\label{eq: ex_1d_ans_coulomb}
\end{align}
である。
Gaussの法則を用いた解法
次はGaussの法則を用いて、無限長一様帯電棒のつくる電場を求める。問題設定は同じ。
【問題】
$z$軸上にある細い針金に一様に帯電させ、単位長さあたりの電荷の線密度を$\lambda$とする。このとき、$z$軸から距離$R$だけ離れた位置$P$の電場を求めよ。
Gaussの法則では、系の対称性を活かした球面$S$をうまくとることが重要である。今回は系の$z$軸まわりの回転対称性を活かして、$z$軸を中心とした長さ$\ell$、半径$R$の円筒表面を$S$とする。
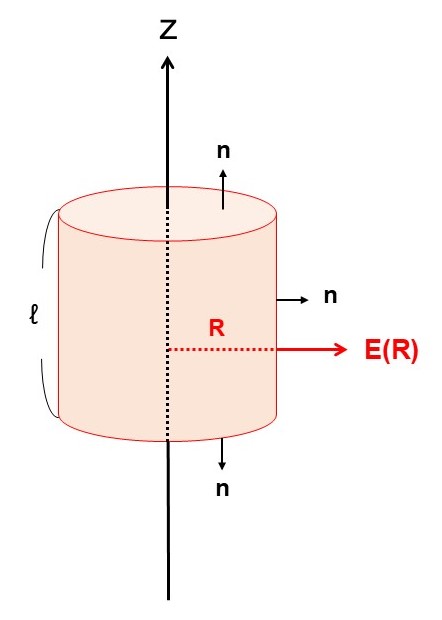
このとき、電場は系の対称性から円筒の側面に直交し、$\bm{E}=E(R)\bm{e}_R$と書ける。
よって，
\begin{align}
\int_S \bm{E}\cdot \bm{n}\, \dd S=E(R)\cdot 2\pi R\ell
\end{align}
である。円筒の上面と底面では電場と法線ベクトルが直交するため内積はゼロである。
一方で、この表面$S$に囲まれる総電荷は$\lambda \ell$である。
Gaussの法則より，
\begin{align}
E(R)\cdot 2\pi R\ell=\frac{\lambda \ell}{\varepsilon_0}
\end{align}
となり、
\begin{align}
E(R) = \frac{\lambda}{2\pi \varepsilon_0 R} \label{eq: ex_1d_ans_gauss}
\end{align}
となる。
先にCoulombの法則で求めた式\eqref{eq: ex_1d_ans_coulomb}の結果とたしかに一致する。
静電ポテンシャル
問題設定はこれまでと同じだが、今回は静電ポテンシャルを求める。
【問題】
$z$軸上にある細い針金に一様に帯電させ、単位長さあたりの電荷の線密度を$\lambda$とする。このとき、$z$軸から距離$R$だけ離れた位置$P$の静電ポテンシャルを求めよ。
電場は次のように書けることを2通りの解法を用いて示した。
\begin{align}
\bm{E}(R) = E(R)\bm{e}_R= \frac{\lambda}{2\pi \varepsilon_0 R}\bm{e}_R
\end{align}
一方で、これは静電ポテンシャル$\phi(R)$と次の関係がある。
\begin{align}
E(R)=-\frac{\partial\phi(R)}{\partial R}
\end{align}
よって、$R$について積分することで、
\begin{align}
\phi(R)=-\int E(R)\, \dd R=- \frac{\lambda}{2\pi \varepsilon_0}\ln R+C
\end{align}
を得る。ただし、$C$は積分定数である。つまり、積分定数の分だけ静電ポテンシャルは不定性がある。静電ポテンシャルの絶対値に意味はなく、周囲との相対的な大小関係によって勾配をつくり、それが電場となる。一般には無限遠をゼロに基準を決めることが多いが、今回は無限遠$(R\to\infty)$において、
\begin{align}
\lim_{R\to\infty}\phi(R)=\infty
\end{align}
となるため、無限遠点を基準にとることができない。そこで、$\phi(R=1)=0$のように基準をとることに決めれば、$C=0$となり、
\begin{align}
\phi(R)=-\int E(R)\, \dd R=- \frac{\lambda}{2\pi \varepsilon_0}\ln R
\end{align}
とすることができる。この基準の決め方は、境界条件が定められていなければ自由である。
コメント